A multiplicative inverse for a (mod n)
Modular Arithmetic
Definition 5
?Let n ∈ N and let a,b ∈ Z. We say that a is congruent to b modulo n?
if n|(a?b).?
We write this as a ≡ b (mod n).
Theorem 2
Let n∈N and let a,b∈Z. TFAE:("The Following Are Equivalent")
1. a≡b(modn).
2. a and b leave the same remainder when divided by n.?
3. a=b+kn?for some?k∈Z.
Theorem 3
Let a1,a2,b1,b2 ∈ Z, and let n ∈ N.?
Suppose, further, that a1 ≡ a2 (mod?n) and b1 ≡b2 (mod?n). Then
1. a1 + b1 ≡ a2 + b2 (mod n).
2. a1b1 ≡ a2b2 (mod n).
3. a1 ? b1 ≡ a2 ? b2 (mod n).

Ok, this is pretty great, but it’s missing one operation! How do we perform division modulo n? Or even, can we?


As a reminder of how we defined division way back when, we had the following definition for the number 1/n?:
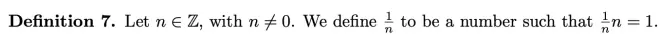
Definition 8
Let n ∈ N and let a ∈ Z. We say that u is?
if?au ≡ 1 (mod n).
So, in Example 8, we showed that 5 is a multiplicative inverse for 3 modulo 7.?
Let’s take a look at another example:

So sometimes inverses exist, and sometimes they don’t.?


There are common?factors between??6? and (2, 3, 4,6).

There are common?factors between? 7?and 7.

There are common?factors between? 8?and (2,4,6,8).
Examining the above 3 examples, you might notice a pattern: multiplicative inverses do not exist anytime the number we are interested in shares a factor with the modulus. This, in general, is the feature we are looking for.
Theorem 4.?
Let n ∈ N and a ∈ Z. Then a has a multiplicative inverse modulo n?
if and only if a ⊥ n.
example:
1?⊥ 6
5?⊥ 6
1?⊥ 7
2?⊥ 7
3?⊥ 7
4?⊥ 7
5?⊥ 7
6?⊥ 7
1?⊥ 8
3?⊥ 8
5?⊥ 8
7 ⊥ 8

