Infinite Series

Theorem 1.?Properties of limits by definition.

Definition 1.?Bounded above and least upper bound property.

Theorem 2?(Heine-Borel).

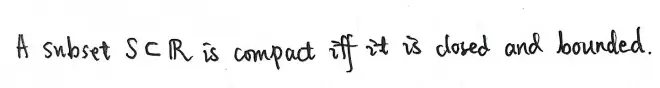
Theorem 3?(Bolzano-Weierstraβ).?A bounded real sequence has convergent subsequence.

Theorem 4.?A real Cauchy sequence is convergent.

Proof.?

Theorem 5.?

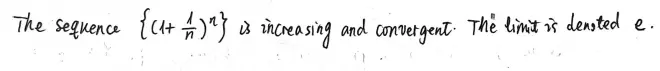
Definition 2. Supremums and infimums, upper and lower limits.

Theorem 6.?

Theorem 7.?e is irrational.

Definition 3.?Partial sum and series, convergence and divergence of series.

Theorem 8.

Note that the converse statement is obviously not true.

Proof.

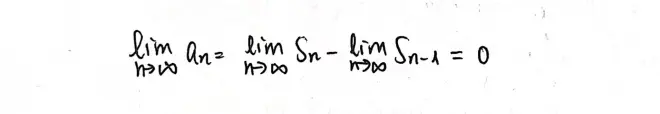
Theorem 9.

Proof. (Sketch)

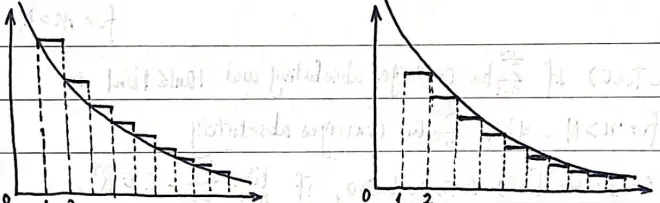
Theorem 10 (2^n test).

Theorem?11?(Alternating test).

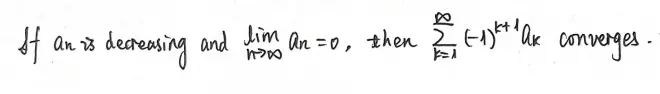
Definition 4.?Absolute convergence and conditional convergence.

Theorem?12?(Comparison?test).

Note that the series does not have to start from n=1, since we can split the first few terms out as a constant, which does not affect convergence.

Theorem?13?(Limiting comparison?test).

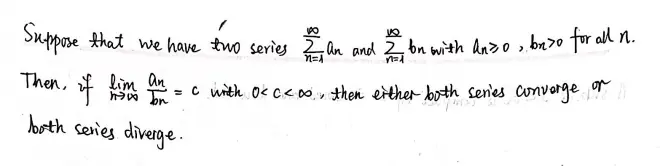
Proof.

Theorem?14?(Euler 1735).

References:?

Chapter 3 of Principles of Mathematical Analysis, 3rd Edition, by Walter Rudin.

Chapter IV of Foundations of Mathematical Analysis, R. Johnsonbaugh and W. E. Pfaffenberger (Dover, 2010).

Theorem 15 (Ratio test).

Proof. For part (b), it can be easily seen that an -> 0 does not hold, so the series diverges.

For part (a),

Theorem 16?(Root test).

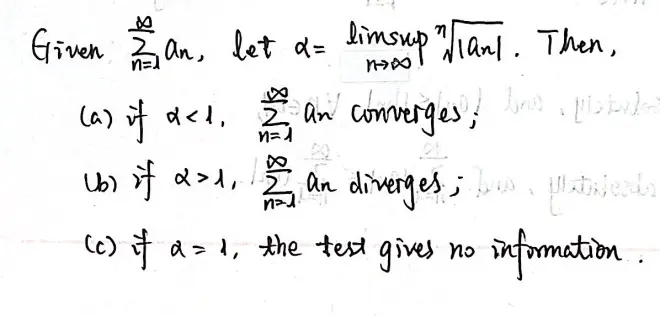
Proof. For part (c), we may consider the series of n^(-1) and n^(-2), one of which diverges and the other one converges.

For part (a) and (b),

Definition 5 (Power series).

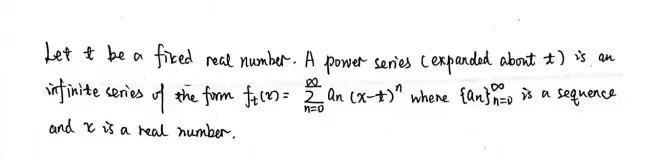
Example 1.

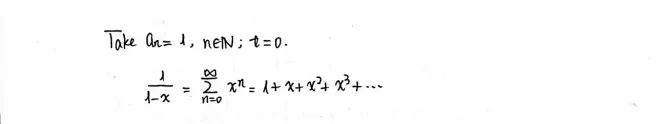
Example 2.

Example 3.

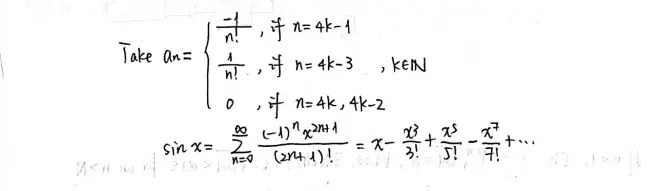
Theorem 17.

Remark 1. The ratio test is frequently easier to apply than the root test, since it is usually easier to compute ratios than the n-th roots. However, the root test has a wider scope. More precisely: Whenever the ratio test shows convergence, the root test does too; whenever the root test is inconclusive, the ratio test is too. Neither of the two tests is subtle with regard to divergence. Both deduce divergence from the fact that an does not tend to 0 as n -> ∞.

Theorem 18.?

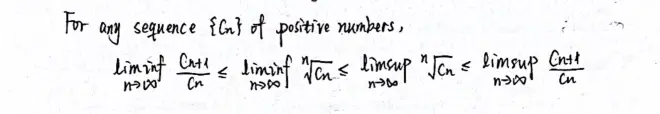
Proof.

Corollary 1.

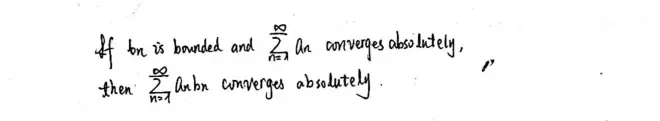
Note that it follows directly from Cauchy's criteria.

Lemma 1.

Proof.

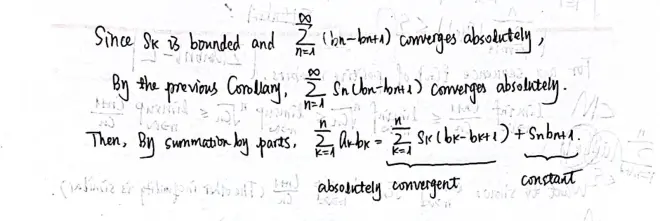
[Revision] In the last line of the proof, it should be "convergent" instead of "constant".

Fact 1?(Summation by parts).

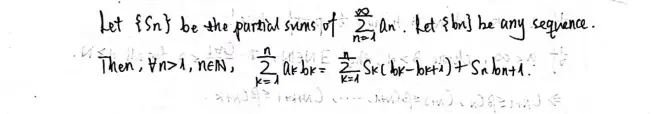
Proof.

Theorem 19?(Dirichlet's test).

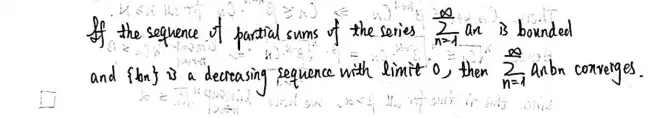
Proof.

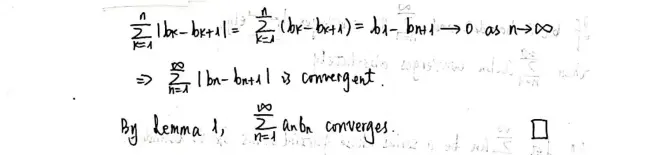
Lemma 2.

Proof.

Theorem 20?(Cauchy product).

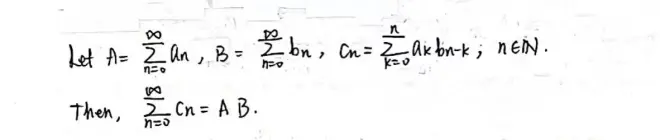
Note that at least one of the two series an or bn must be convergent absolutely.

Proof.

If there exists any?infringement within this article (note), please inform me and I will delete it at once.